One of the basic tenets of quantum mechanics is that
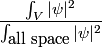 is the probability that the particle is in the volume 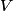 (assuming that (assuming that 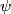 is normalizable). In is normalizable). In 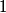 dimension, this becomes dimension, this becomes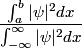 In our case, 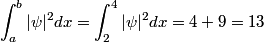 and 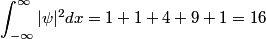 Therefore, the answer is 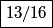 . So, answer (E) is correct. . So, answer (E) is correct. |
One of the basic tenets of quantum mechanics is that
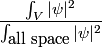 is the probability that the particle is in the volume 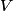 (assuming that (assuming that 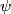 is normalizable). In is normalizable). In 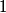 dimension, this becomes dimension, this becomes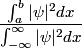 In our case, 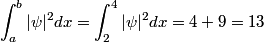 and 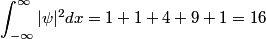 Therefore, the answer is 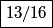 . So, answer (E) is correct. . So, answer (E) is correct. |